Микромир и макромир

Экспериментально установлено, что поведение микроскопических объектов невозможно объяснить привычными нам законами физики макромира. В начале двадцатого столетия для описания явлений микромира была предложена другая физика - квантовая механика. Законы квантовой механики для нас (жителей макромира) крайне необычны, очень часто знакомство с ними вызывает неприятие, они довольно сложны математически и далеко не всегда поддаются переводу с языка формул и уравнений на язык понятий и удобных для человека образных представлений. Квантовая механика очень плоха, обычно студенты ненавидят этот предмет. У квантовой механики есть всего одно достоинство: она с высокой точностью объясняет поведение микромира и обладает положенной хорошей научной теории предсказательной силой. Поэтому и приходится мириться с множеством ее недостатков, перечисленных выше.

Квантовая механика "объемнее" обычной классической механики. Классическая физика выводится из квантовой механики как частный случай, когда размеры объектов достаточно велики и квантовыми эффектами можно пренебречь.

Я не считаю необходимым (да и возможным) в пределах этого курса давать системное изложение квантовой механики. По мере необходимости я буду обращаться к ее аппарату, стараясь обходиться без математики. Для начала полезно будет дать некоторое сравнение наиболее важных свойств макромира и микромира.

1. Макрообъекты имеют определенный размер. Микрообъекты не имеют размера.

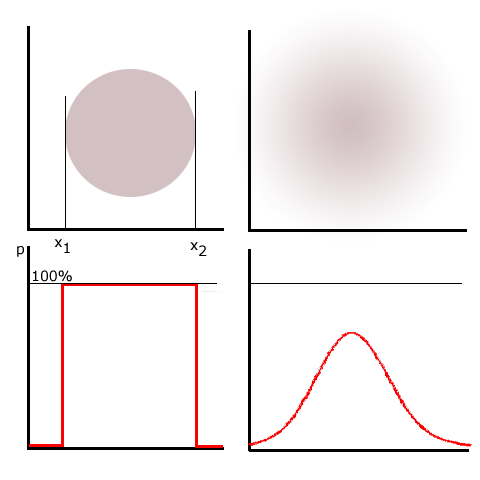
Я всегда могу сказать, что некая макроскопическая сущность имеет точно очерченные границы. Макроскопический круг на левом верхнем рисунке начинается по оси Х в точке х₁ и заканчивается в точке х₂. Можно уверенно сказать, что левее точки х₁ его нет, потом на отрезке [x₁, x₂] он есть, а правее точки х₂ его снова нет. Тоже можно выразить языком вероятности (график под левым кругом): левее точки х₁ вероятность обнаружения круга равна нулю, на отрезке [x₁, x₂] она равна 100%, а правее точки х₂ - снова ноль.

Совсем иначе ведет себя круг в макромире (рисунок справа сверху). Совершенно невозможно сказать, что он начинается и заканчивается в определенной точке. Он "размазан" по всей Вселенной. Вероятность обнаружить его на бесконечно большом удалении в любом направлении никогда не бывает равной нулю. Но и вероятность обнаружения его в самом центре рисунка меньше ста процентов. Микроскопический объект находится сразу везде, но при этом он нигде не находится полностью. И график его вероятности (под кругом справа) имеет форму колокола, нигде не достигающего нуля.

Замечание №1: В нашем макроскопическом мире тоже существуют объекты, не имеющие очерченных пространственных границ. Например, у облака нет очерченных границ. Тем не менее функция вероятности нахождения облака в пространстве убывает у его границ достаточно резко (см. рис ниже), поэтому я всегда могу определить границы облака приблизительно, но с вполне удовлетворительной точностью. В микромире точность границ будет настолько неудовлетворительной, что сами границы не будут иметь смысла.

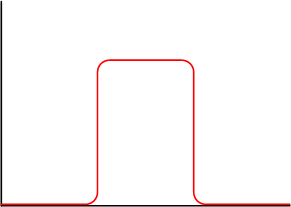
Замечание №2: На самом деле, в нашем мире функция вероятности никогда не изменяется мгновенно от нуля до ста процентов. То есть, я никогда не могу определить бесконечно малую линию или плоскость, по которой проходит граница предмета - она всегда будет немножко размазана. Но эта размазанность настолько невелика (скажем, с полмиллиметра для того стола, за которым я сейчас сижу), что в практическом смысле она не имеет значения. Хотя токарь, вытачивающий втулку для вставки в отверстие со мной не согласится. Пара "соток" (0.01 мм) не в ту сторону - и втулка никогда не войдет туда, куда ей положено войти. Но все равно, эта неопределенность намного-намного меньше неопределенности границ в микромире.

Замечание №3: На всех рисунках показаны одномерные функции вероятности, только вдоль оси Х. На самом деле наше пространство не одномерно. Но мне с моими "художественными способностями" многомерную функцию вероятности точно не нарисовать.

2. Движение макрообъектов детерминировано. Движение микрообъектов вероятностно

Для любого движущегося объекта в макромире существует понятие траектории - маршрута движения. Траектория может быть очень простой, например, прямолинейной, или очень сложной, но она существует. А поскольку она существует, ее можно рассчитать, зная координаты и их производные по времени (скорости, ускорения и производные более высоких порядков). Даже если на практике такой расчет окажется неимоверно сложным, это - лишь техническое затруднение. Имея достаточно точную измерительную аппаратуру и достаточно мощные считающие устройства, мы сможем решить эту задачу. В микромире само понятие траектории лишено смысла. Микрообъект вероятностен, и его движение тоже вероятностно. Принципиально невозможно определить, где будет находиться микрообъект в каждый момент времени, можно лишь оценить вероятности его нахождения в различных точках пространства в различные моменты времени. Причем чем точнее мы определим местонахождение, тем более размазанным окажется время, и наоборот.

3. В макромире частицы и волны различны. В микромире любой объект имеет волновые и корпускулярные свойства, то есть является одновременно волной и частицей

Два макроскопических шарика могут столкнуться друг с другом и вновь разлететься после столкновения. В полном соответствии с законом сохранения импульса, "управляющим" столкновениями частиц. Две макроскопических волны могут пройти друг сквозь друга, никак не прореагировав на "столкновение", а могут интерферировать, когда в одних точках они взаимно уничтожатся, в других - усилятся, в третьих - изменятся как-то еще. Взаимодействие двух макроскопических волн описывается уравнениями волновой физики. Корпускулярный закон сохранения импульса неприменим к волнам, а волновые уравнения неприменимы к частицам.

Два микрообъекта (например, два электрона) могут пройти друг сквозь друга, но при этом их их импульсы могут измениться (или не измениться) в соответствии с волновыми уравнениями. Взаимодействия микрообъектов описывается одними и теми же уравнениями безо всякого деления на волны и частицы. Электрон - и волна, и частица (и что-то еще сверх того). То же верно в отношении остальных микрообъектов.

4. В макромире барьеры бывают непреодолимыми. В микромире любой барьер преодолим с некоторой вероятностью

Если поместить макроскопический шарик между двух стенок бесконечной высоты, заставив его прыгать от одной стенки к другой, шарик никогда не сможет преодолеть барьеры. Разве что его кинетической энергии хватит на то, чтобы пробить в одном из них дыру, или высота окажется не бесконечной. Если в аналогичную ситуацию попадает микроскопический объект, он пройдет сквозь барьер при любой высоте барьера и любой собственной энергии. Правда, с определенной вероятностью, которая может оказаться настолько малой, что мы не сможем ее обнаружить. И шарик за пределами барьера тоже не сможем обнаружить. Но это - проблемы ограничение не шарика, а наблюдателя. И на этом странном и таком далеком от реальной жизни прохождении электронов сквозь барьеры основаны, среди прочего, все наши с вами компьютеры и множество другой электроники.