Между возможным и реальным (о кинетике и термодинамике)

Значение свободной энергии показывает возможность или невозможность протекания процесса. В пределе (то есть через бесконечно долгий промежуток времени) процесс обязательно пойдет именно туда, куда ему "велит" пойти термодинамика, а именно, в том направлении, для которого параметр ΔG принимает наиболее отрицательное значение. Однако в нашем коротком временном масштабе этот переход может и не произойти. Это - несомненное жульничество, которым мы, представители homo sapiens, пользуемся на каждом шагу. Например, твердая сталь термодинамически устойчива лишь при температуре выше 912ºС. При более низких температурах она термодинамически обязана превратиться в мягкое железо. Однако этот процесс требует немалого времени, поэтому не только недавно выпущенные инструменты, но и средневековые и даже античные мечи все еще сохраняют твердость. Она сохранится, как минимум, еще несколько тысячелетий - намного больше, чем "расчетное время жизни" изделия.

Насколько можно понять, сама жизнь (и мы с вами, как частный случай ее проявления) термодинамически не разрешены. Однако, ничего, живы пока что.

Тем, как именно происходит практическая реализация процесса, с какой скоростью и при каких условиях он протекает, занимается не термодинамика, а совсем другой раздел физической химии - кинетика. Попробуем разобраться с некоторыми концепциями кинетки, которые необходимы нам для дальнейшего обсуждения.

В подавляющем большинстве случаев процесс идет сложным путем. На пути к термодинамически устойчивому состоянию система проходит много "промежуточных станций". Каждая такая "станция" носит название метастабильного состояния, поскольку энергия системы непосредственно до и непосредственно после метастабильного состояния выше.

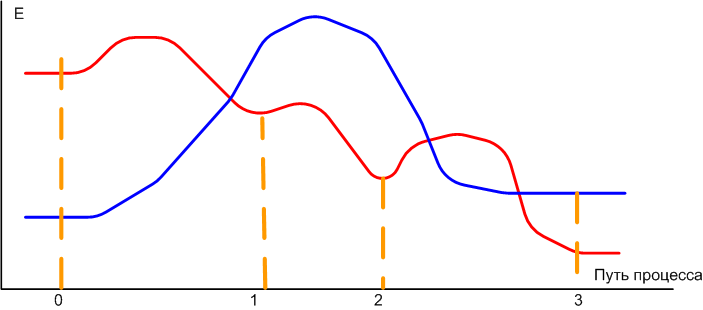
На рисунке схематически показаны два пути процесса, синий и красный. "Красный процесс" начинается с исходного состояния (обозначенного "0" на оси пути процесса), энергия которого имеет некоторое значение. По дороге к конечному состоянию 3 процесс проходит метастабильные состояния 1 и 2. Между любыми двумя минимумами энергии (0, 1, 2, 3) имеются максимумы. Для того чтобы система прошла, например, из состояния 0 в состояние 1, ей требуется некоторый избыток энергии, без которого она никогда не преодолеет горку между этими двумя точками. Обратите внимание: переход 0 → 1 выгоден термодинамически, поскольку энергия состояния 2 ниже энергии состояния 1. Однако без резерва энергии система не перейдет в более выгодное для нее состояние. Аналогично переход из состояния 1 в состояние 2, или из 2 в 3 тоже требует резерва энергии.

В жизни нередко случается, что из-за отсутствия необходимой для перехода энергии система может застрять в термодинамически не самом выгодном состоянии на очень долгое время. Именно поэтому такие состояния и называются метастабильными. Термодинамически они невыгодны, но кинетически - вполне ничего.

Если посмотреть на путь "синего процесса", то нетрудно увидеть, что термодинамически он вообще не должен происходить, потому что энергия конечного состояния выше, чем начального. Однако такой процесс возможен кинетически - все дело в высоте барьера, который не пускает систему вернуться в более выгодное термодинамически исходное состояние. Это, кстати, как раз и есть случай со сталью. Когда сталь варят, то при температуре намного выше 912ºС образуется твердая разновидность (так называемое гамма-железо). Температура процесса высока, поэтому резерв энергии вполне достаточен для перехода через потенциальный барьер. Затем сталь начинают охлаждать. Энергия системы падает быстрее, чем твердое гамма-железо переходит в мягкое альфа-железо. В конце процесса охлаждения мы имеем твердое гамма-железо, застрявшее в метастабильном состоянии. Если эту сталь подогреть градусов так до восьмисот на пару-тройку часов, энергии будет достаточно и все гамма-железо перейдет в альфа-железо. Но при обычной температуре этот процесс идет очень медленно, с точки зрения короткой человеческой жизни, бесконечно долго.

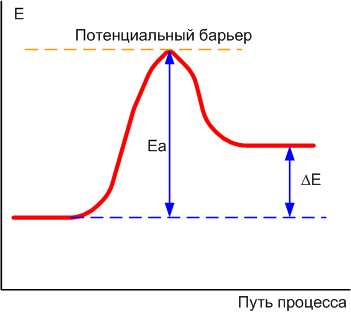
Барьер, который отделяет друг от друга метастабильные (или просто стабильные) состояния, называют потенциальным барьером (или барьером потенциала). А та энергия, которую нужно иметь для преодоления потенциального барьера, называется энергией активации Ea.

Обратите внимание: энергия активации Ea - это совсем не то, что изменение энергии в результате процесса ΔE (или ΔG).

Что интересно, процесс преодоления потенциального барьера носит вероятностный характер. Дело в том, что частицы, из которых состоит система, могут обмениваться энергией. Поэтому несколько частиц могут, например, в результате соударений, "скинуться" и снабдить одну частицу вполне достаточным для преодоления барьера количеством энергии. И эта частица перейдет через барьер. Но зато оставшимся будет еще труднее его преодолеть - ведь они отдали часть своей энергии, и теперь у них ее еще меньше. Понятно, что если в систему вносить извне энергию (например, нагревом, облучением или любым другим способом), общее количество энергии частиц начнет расти, а вероятность перехода через барьер - повышаться. Пока не станет равна ста процентам. Собственно, именно это мы делаем, нагревая систему, чтобы заставить ее прореагировать.

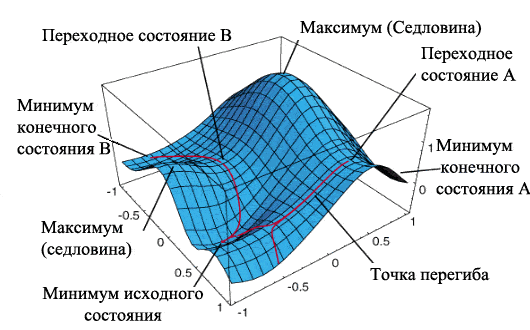
Остается лишь добавить, что в реальных процессах путь идет не в системе двух координат, а в намного более сложном многомерном пространстве. В качестве иллюстрации можно привести трехмерную потенциальную поверхность некоторого процесса, который может пойти по одному из двух различных маршрутов А или В:

Трехмерная потенциальная поверхность ни в коем случае не является пределом. Вообще говоря, пространство потенциалов имеет столько измерений, сколько степеней свободы есть у системы (у системы из N частиц может быть до (3N - 5) степеней свободы). Но это усложняет только изображение и расчет. Суть остается той же, что и для двухмерных профилей в начале нашего обсуждения.